[(COMP472)Artificial Intelligence] - Uninformed Search | BFS | DFS | Iterative Deepening | Uniform-Cost Search

< Uninformed Search >

: all nodes are equally optimistic, so we explore them systematically

=> Simple search method, without heuristics or information, explores all possible paths.

 

·    Data Structure

-       Open List(=frontier)

-       Closed List(=explored set)

 

 

·    Generic Search Algorithm

1)    Initialize OPEN with the initial node n0 and its parent

2)    Initialize CLOSED to empty

3)    Repeat

       A)    If OPEN is empty, then exit with failure 

       B)    Else,

             (1)   Remove the first node n from the OPEN list

           

             (2)   If n is a goal state

                    (a)  Extract the solution path from n to n0 following the chain of parents

                    (b)  Exit with success      

 

             (3)  Else, 

                   (a)   Generate the successors of n

                   (b)  Insert n in CLOSED

                   (c)   For each successor s of n, depending on the specific search algorithm

                          (i)  Check if s is already in OPEN or in CLOSED

                               - BEFORE inserting a node s what to check in OPEN and CLOSED depends on the specific search                                        algorithm

                         (ii)  Determine if <s, n> should be inserted in OPEN and in what order.

                              - Once we determine that a node s should be inserted in OPEN, 

                                 The order of the nodes in OPEN depends on the specific search algorithm

 

 

 

[ Breadth-First Search ]

: visit siblings before successors

-       Visit level by level

-       Open list is a queue

 

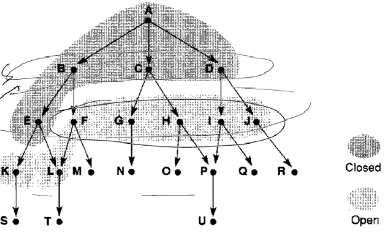
=> Optimal, always find the shortest solution

=> BUT, high memory requirement

 

 

[ Depth-First Search ]

: visit successors before siblings

-       Visit branch by branch

-       Open list is a stack

=> Require less memory, memory efficient! 

=>  BUT, no guarantee to find the solution path

 

 

 

[ Depth-limited Search ]

: compromise for DFS (less memory)

-       Do DFS with depth cutoff k

-       Possible outcomes : solution/failure(no solution) /cutoff (no solution)

 

 

 

[ Iterative Deepening ]

: combination of BFS and DFS (less memory & optimal)

-       do DFS with a maximum depth before going to next level

 

 

 

[ Uniform-Cost Search ]

: edges(actions) have different costs, guarantees to find the lowest cost solution path.

 

-       Uses OPEN as a priority queue (similar as BFS)

-       BUT, OPEN queue sorted by the total cost from the root to node n (g(n))

 

=> only use g(n)- lowest cost, h(n) = 0(Uninformed Search, but admissible)

( Admissible means all node is h(n) < h*(n))