Code&Data Insights
[Machine Learning] Linear Model - Linear Regression | Logistic Regression | Multiclass Logistic Regression | Linear Basis Function Models 본문
[Machine Learning] Linear Model - Linear Regression | Logistic Regression | Multiclass Logistic Regression | Linear Basis Function Models
paka_corn 2023. 6. 14. 07:53Linear Model
- Easy to optimize, fast training and prediction
- Good Interpretability
- ONLY suitable for linearly separable classes
=> The capacity of the linear model depends on the input dimensionality D.
=> VC dimensions : D + 1 for Logistic regression
VC dimension?
: a measure of the capacity or complexity of a hypothesis space
Linear Regression

- Parameter space is convex
- Objective function : MSE
- Can find the closed form
=> We can use the analytical solution without using gradient descent!
· Analytical Solution


=> Direct Solution

Logistic Regression

- Logistic Regression = Binary Classification
· Why We Use Squashing Function?
- To makes sure the output is bounded between 0 and 1. (probability)
=> Use Sigmoid (Logistic Function)

=> derivative of sigmoid

- Draw linear boundaries between two classes
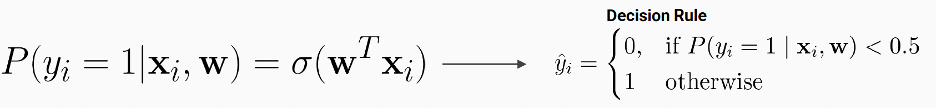
- Decision boundaries are all those points where there is maximum uncertainty
=> Maximum uncertainty :
- In Logistic Regression, the direct closed-form solution does not exist!
-> Train logistic regression with Gradient Descent
-> Define Objective Function
-> Compute the gradient of the loss function
- Objective Function: Binary Cross Entropy


Multiclass Logistic Regression
: a machine learning model that outputs K probabilities.
- Linear Transformation + SoftMax
=> SoftMax – squashing function
· Why We Use Squashing Function?
- To makes sure the output is bounded between 0 and 1. (probability)
- The sum of all the K probabilities is 1.
- The softmax introduces competition within the output units: the increase of one probability leads to a decrease in the others.
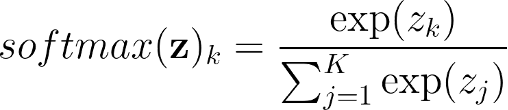
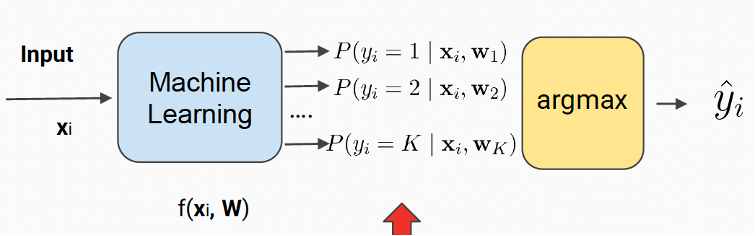
-> Argmax: select the class with the highest probability
- Train Multiclass Logistic Regression,
1) Define a objective(loss) function
=> Categorical Cross Entropy(CCE) = NNL

2) Compute the gradient of the loss to update the parameters
=> Derivative of CCE
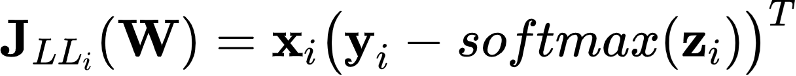
- Optimization space for Logistic Regression & Multiclass Logistic Regression
=> The optimization space is convex, so it’s good for optimization

Linear Basis Function Models
: transform the input features to make the classes linearly seperable
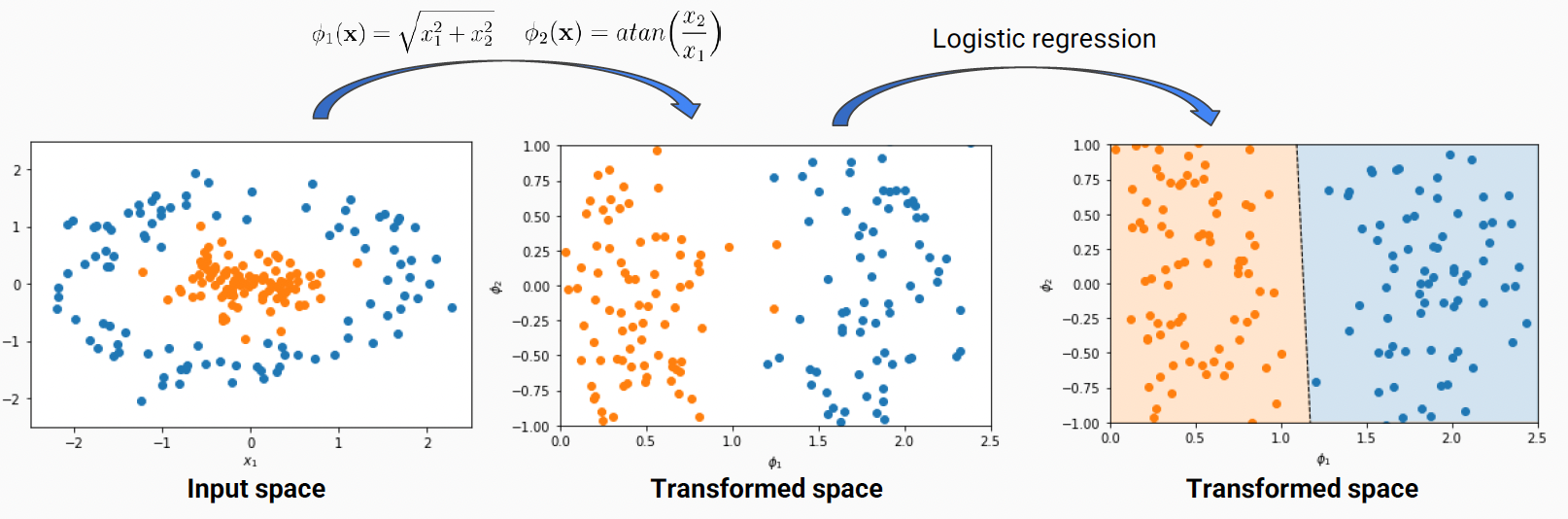


<- Manually engineer this, NOT EASY!
BUT, transformation by hand is NOT easy task!
=> a challenging task that requires a lot of domain-specific human knowledge

--> Why Not we learn this from data?
==> Neural Network ( Fully data-driven )



