[Data Structure] Trees, Binary Trees

* What is Tree in Data Structure? 

:  non-linear and an abstract model of a hierarchical data structure. parent-child relation

(ex) Organization charts, File Systems, Programming environments

 

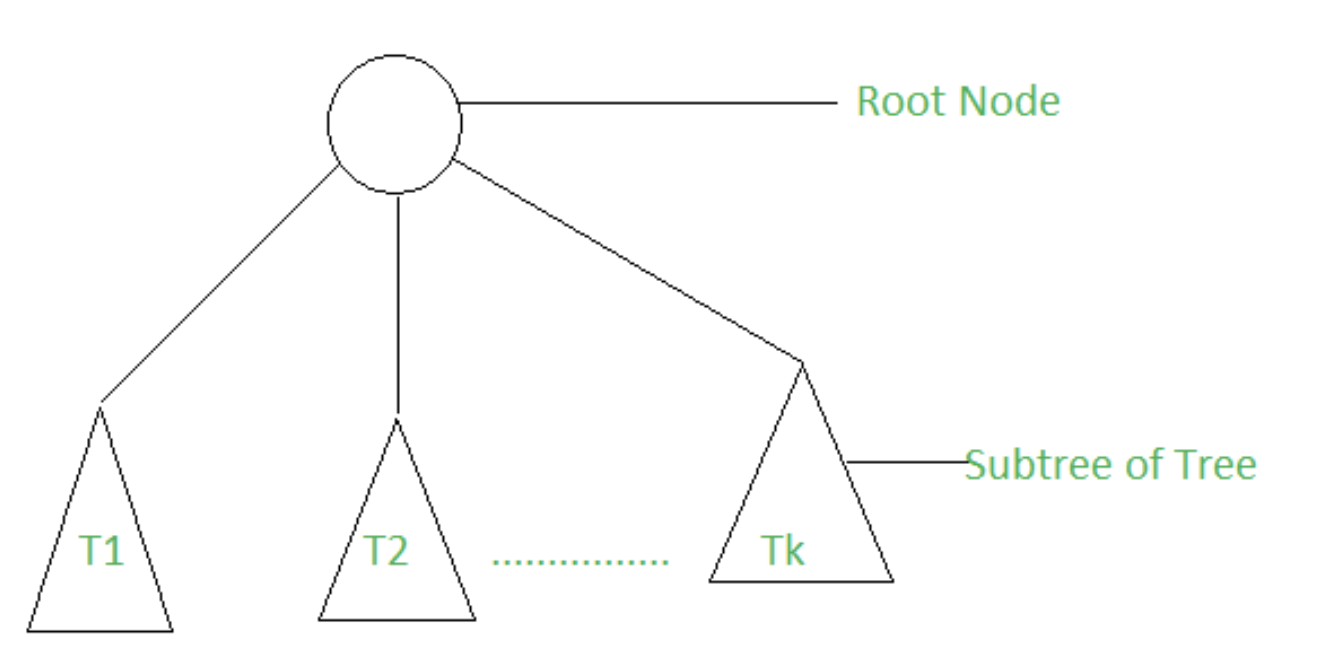
* Tree Traversals 

(1) PreOrder Traversal:  Root - Left - Right

 

Algorithm preOrder(x)

          visit(x)

          for each child y of x

                   preorder(y) 

 

(2) PostOrder Traversal: Left- Right - Root 

 

Algorithm postOrder(x)

          for each child y of x

                   preorder(y) 

          visit(x)

 

InOrder Traversal: Left - Root - Right

 

(3) InOrder Traversal: Left- Root - Right

 

 

 

* Types of Tree data structures

1) General Tree

: 모든 노드가 무한대 수의 자식 노트를 가질 수 있다. 

Every node may have infinite numbers of children. 

2) Binary Tree

: Most two children can be found for each parent. ( 최상위 루트 노드가 가질 수 있는 자식의 노드수가 2개 이하)

- Perfect Binary Tree

: It has the maximum number of nodes. 

: height h, the maximum number of nodes = 2^(h+1) -1

=> h = log(n+1) -1

 

- Complete Binary Tree

: All leaves have the same depth, the last level of nodes does not need to be completely full. 

: number of nodes at depth d = 2^d

: height of the tree = log(n+1)

 

- Euler Tour Traversal 

: Informally described as a "walk around" the tree, where every node is traversed 3 times

(on the left, from below, and on the right)

 

3) Balanced Tree 

: the difference between the heights of sub-trees of any node in the tree is not greater than one. 

 

 

- Balanced Binary Tree

: Since height is always logN, the Time complexity of Search() is in B.Tree is always O(logN). 

=> 보통의 이진트리(binary tree)는 노드가 한쪽으로 치우쳐질 가능성이 있기때문에 탐색 시간은 O(n). 

 

500

 

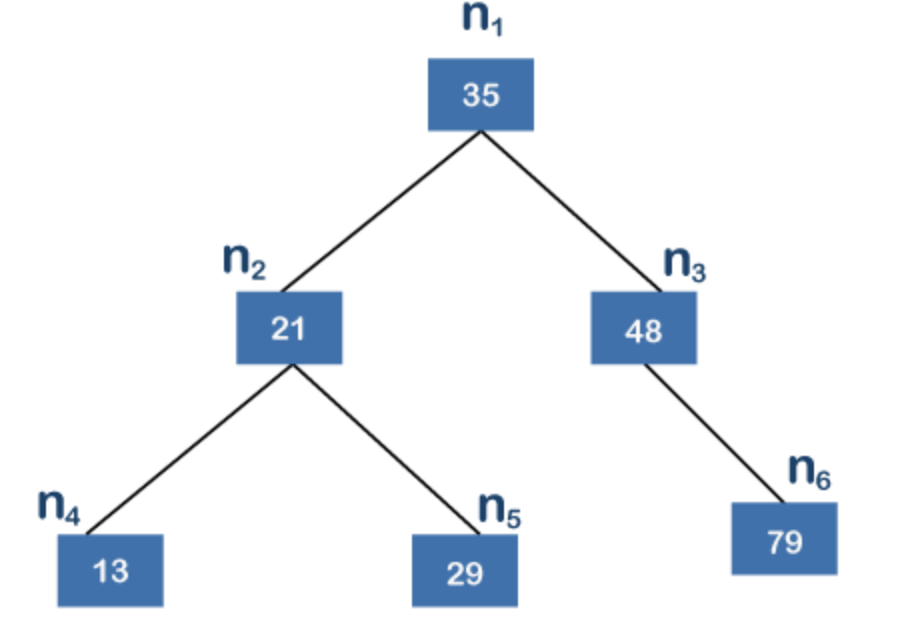
4) Binary Search Tree 

:  Extension from Binary Tree, it is efficient for fast lookup, addition, and removal of data items since the data is allocated by the value of the node. ( 데이터 값(크기)에 따라 자리가 정해지기 때문에, 자료의 탐색,삽입, 그리고 삭제에 효율적이다.)

( binary search = 자료를 계속 반으로 나누어 가며 검색하는 방법 )

 

: A binary search tree(BST) is called an ordered or sorted binary tree. 

The amortized time for the insert, delete and search take O(log N) for n nodes.

 

* Examples of Application

(1) Sort

- BST is used in sorting algorithms such as tree sort, quick sort

: 

 

(2) Priority Queue Operations

 (Priority queue를 implementation 하기 위한 방법은 list, array, heap, BST가 있지만, heap이 가장 efficient함)

 

- BST is used in implementing priority queues, using the node's key as priorities. 

 

: If it is an ascending order priority queue, the removal of an element with the lowest priority is done through leftward traversal of the BST.

: If it is a descending order priority queue, the removal of an element with the highest priority is done through rightward traversal of the BST.

 

 

 

 

 

 

reference : 

https://www.geeksforgeeks.org/introduction-to-tree-data-structure-and-algorithm-tutorials/

https://www.geeksforgeeks.org/complete-binary-tree/#:~:text=Properties%20of%20Complete%20Binary%20Tree%3A%201%20A%20complete,levels%20except%20the%20last%20level%20are%20completely%20full.

https://www.baeldung.com/cs/height-balanced-tree